05. 前馈过程
前馈
假设只有一个隐藏层,我们在计算中会需要两个步骤。第一个是计算隐藏状态的数值,第二个是计算输出值。
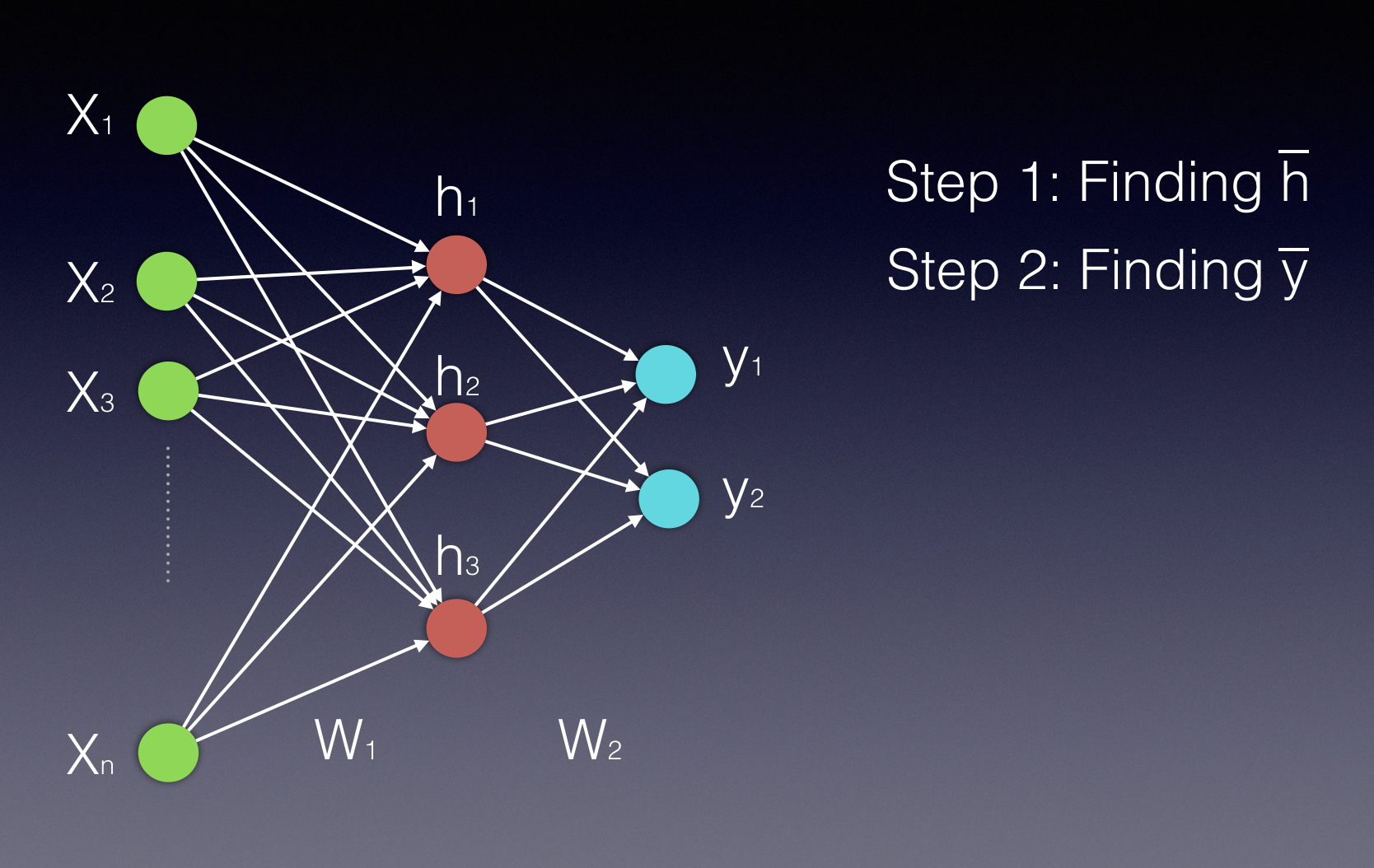
请注意,隐藏层和输出层都显示为向量,因为它们都是多个单一神经元表示的。
第一个视频将帮你了解第一个步骤:计算隐藏状态的数值。
06 前馈 A V7 最后一节
正如你在上面视频中所见,将输入向量乘以权重矩阵W^{1},可以计算得到隐藏层的向量{h'},具体如下:
\bar{h'} = (\bar{x} W^1 )
我们在矩阵乘法使用向量,可以看到以下计算:
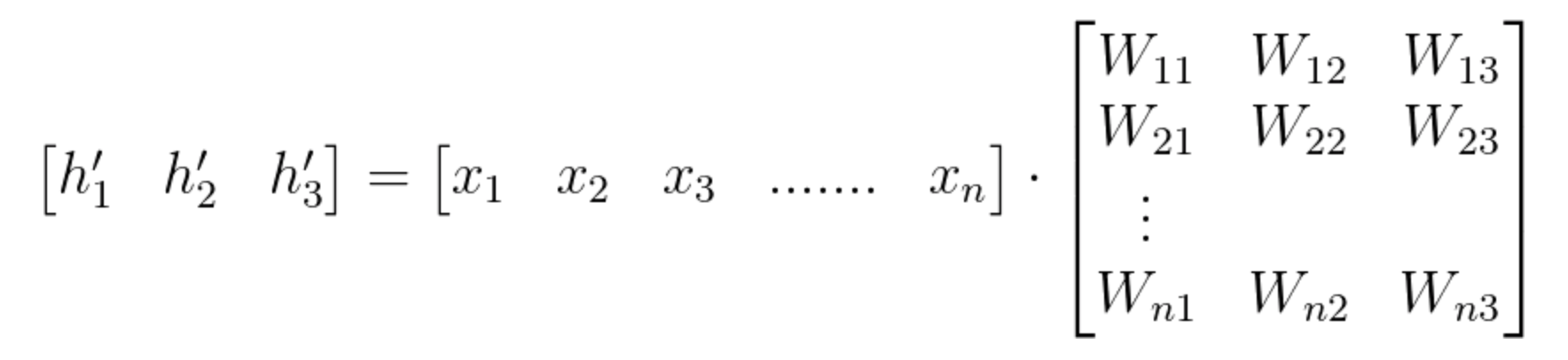
方程式1
我们找到h'后,需要一个激活函数( \Phi)来完成隐藏层数值的计算。这个激活函数可以是双曲正切、Sigmoid或ReLU函数。我们可以使用以下两个方程式来表示最终隐藏的向量\bar{h}:
\bar{h} = \Phi(\bar{x} W^1 )
或
\bar{h} = \Phi(h')
由于W_{ij}
表示权重矩阵中的权重部分,连接输入中的神经元 i 和隐藏层的神经元 j,我们也可以按照以下方式书写计算:
(请注意,在这个例子中,我们有 n 个输入,只有 3 个隐藏的神经元)
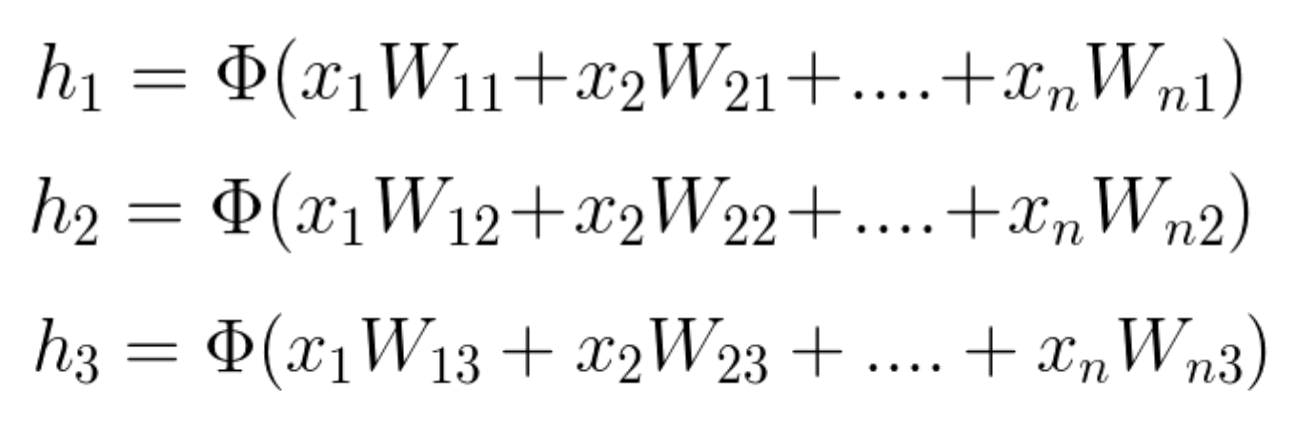
方程式 2
关于激活函数的更多信息以及使用方法可参考此处
下一个视频可以帮你了解第二个步骤:计算输出值。
07 前馈 B V3
正如你在上面的视频中所见,计算输出向量的过程在数学上类似于计算隐藏层向量的过程。我们再次使用一个矩阵乘法的向量,然后使用一个激活函数。通过隐藏层和矩阵计算得出的最新向量,将隐藏层连接到输出起来。
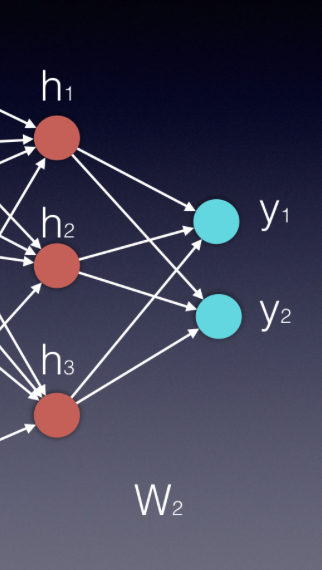
从本质上讲,神经网络中每个新层都是向量乘以矩阵进行计算,其中向量连接了输入和新层,而矩阵连接了新的输入和下一层。
在我们的例子中,输入向量是\bar{h},而矩阵是W^2,所以\bar{y}=\bar{h}W^2。在某些应用中,使用 softmax 函数很有帮助(如果我们希望所有的输出值在 0 到 1 之间,它们总和为 1 )。
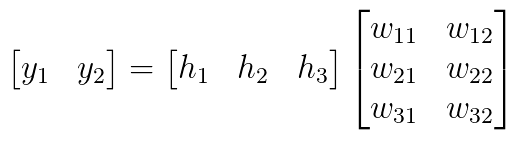
方程式 3
接下来的几个视频将关注反向传播过程,即使用链式法则的随机梯度下降。